Scaling

This page describes routines that deal with scaling data. The Excel form will in have the following two layouts depending on the option the user selects.

Layout A:

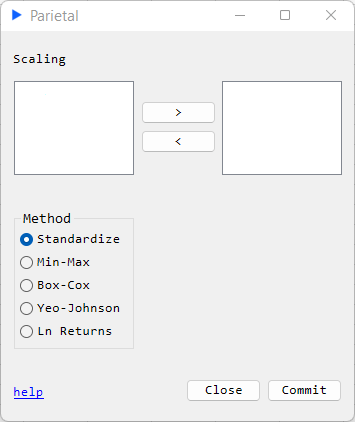
Layout B:

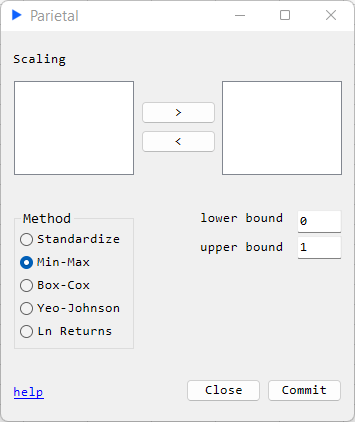
Standardize#

Description#

Return a matrix that is column-wise centered to mean 0 and scaled to a standard devation 1. More precisely, each original $x$ in a column corresponds to the following transformation: $$f(x) = \frac{x - \overline{x}}{\sigma}$$ where $\overline{x}$ is the column mean and $\sigma$ is the column standard deviation.

Returns#

• Matrix with the scaled columns

Min-Max#

Description#

Return a matrix that is column-wise scaled to a lower bound $lb$ and an upper bound $ub$ specified by the user. More precisely, each original $x$ in a column corresponds to the following transformation: $$f(x) = lb + \frac{(x - min(x)) (ub - lb)}{(max(x) - min(x))}$$

Returns#

• Matrix with the scaled columns

Box-Cox#

Description#

Return a matrix that is column-wise scaled using the Box-Cox transform. The transform itself is defined as:

$$y(\lambda)= \begin{cases} \Large\frac{y^{\lambda} - 1}{\lambda} & \text{ if } \lambda\neq 0 \\log(y) &\text{ if } \lambda = 0 \end{cases}$$

An optimization routine is used to find the parameter $\lambda$ maximizing the log-likelihood function for the Box-Cox transform.

Returns#

• $\lambda$ for each column
• Matrix with the scaled columns

Yeo-Johnson#

Description#

Return a matrix that is column-wise scaled using the Yeo-Johnson transform. The transform itself is defined as:

$$y(\lambda)= \begin{cases} \frac{(y+1)^{\lambda} - 1}{\lambda} &\text{ if } \lambda\neq 0, y \geq 0 \\log(y+1) &\text{ if } \lambda = 0, y \geq 0 \\\frac{(1-y)^{2-\lambda} - 1}{\lambda-2} &\text{ if } \lambda\neq 2, y \lt 0 \\-log(1-y) &\text{ if } \lambda = 2, y \lt 0 \end{cases}$$

An optimization routine is used to find the parameter $\lambda$ maximizing the log-likelihood function for the Yeo-Johnson transform.

Returns#

• $\lambda$ for each column
• Matrix with the scaled columns

Log Returns#

Description#

Return a matrix that calculates column-wise natural log returns. $$f(x) = ln\frac{x_{1}}{x_{0}}$$

Returns#

• Matrix