Factor Analysis

If we make the assumption that a set of underlying (or latent) variables is responsible for a large part of the dynamics in the target dataset, then we can use a set of techniques that seek to identify and quantify those underlying variables. While many such techniques exist, one such very widely used one is called Factor Analysis.

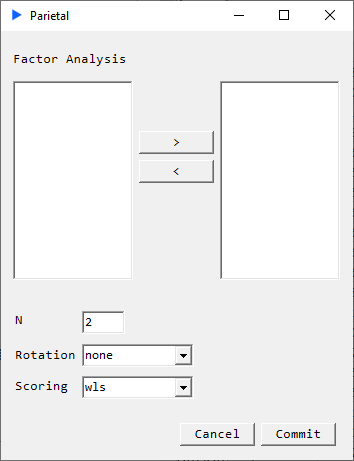
Rotation Options:

• None
• Equamax
• Orthomax
• Parsimax
• Promax
• Quartimax
• Varimax

Scoring:

• WLS
• Regression

N : Number of Components

Description#

The factor analysis model can be described as $$Y = \Lambda F + E$$ where
$\Lambda$ are the factor weights
$F$ are the factor scores
$E$ is the error term

Clearly, a reconstructed approximation of the target dataset can be carried out by $\Lambda * F$. For example, in a single factor model:

$$\begin{matrix} y_1 = \lambda_{1} f_{1} + \epsilon_{1} \\ y_2 = \lambda_{2} f_{1} + \epsilon_{2} \\ y_3 = \lambda_{3} f_{1} + \epsilon_{3} \end{matrix}$$

Returns#

• GoF: Chi-square, p-value, log-likelihood
• Factor Loadings: $\Lambda\$ i.e. weights
• Rotation Matrix
• Factor Scores: $F$
• MLE Variances: