Stochastic Volatility

Time Series Volatility#

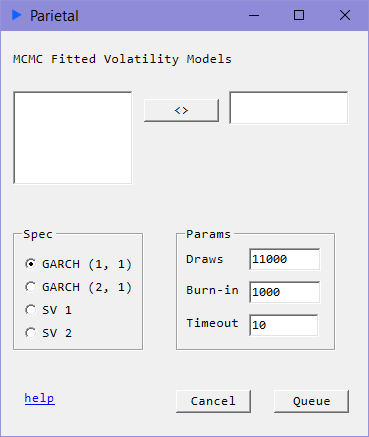
Description#

SV models are state-space models where the volatility process is stochastic. In contrast, the volatility process in GARCH models is deterministic.

Model: SV 1#

$$ y_{t} = \mu + \epsilon_{t}^{y}, \epsilon_{t}^{y} \sim N(0, e^{h_{t}}) $$ $$ h_{t} = \mu_{h} + \phi_{h}(h_{t-1} - \mu_{h}) + \epsilon_{t}^{h}, \epsilon_{t}^{h} \sim N(0, \omega_{h}^{2}) $$

Model: SV 2#

$$ y_{t} = \mu + \epsilon_{t}^{y}, \epsilon_{t}^{y} \sim N(0, e^{h_{t}}) $$ $$ h_{t} = \mu_{h} + \phi_{h}(h_{t-1} - \mu_{h}) + \rho_{h}(h_{t-2} - \mu_{h}) + \epsilon_{t}^{h}, \epsilon_{t}^{h} \sim N(0, \omega_{h}^{2}) $$

Note: Asynchronous Routines#

These routines are asynchronous. Once you hit Queue Job, the request is submitted to the computing engine. You can send as many jobs as you need to the engine queue. Each will run on a separate thread and on any available cores or as they become available. You can periodically check on the status of the job. When it indicates that it is done, you can simply click on the left block of the requested job and hit Fetch. You can also simply terminate the job if you want to by hitting Try Kill.

Input#

• draws: Run the sample this many times.
• burn-in: Discard these many samples from the beginning draws. Burn-in must be less than draws.
• timeout: Time limit in minutes.

Returns#

• coef: Coefficient estimates for $g$ for GARCH parameters and $a$ for ARCH parameters
• serr: Standard Errors
• $ e^{h_{t}/2} $: Volatility Process. Note that the state variable log volatility $ y_{t} | h_{t} \sim N(0, e^{h_{t}}) $ is equivalent to $ y_{t} = e^{h_{t} / 2} \epsilon_{t} $.

Reference#

• Stochastic Volatility: Likelihood Inference and Comparison with ARCH Models (Kim, Shephard, Chib)