Smoothing
This page describes routines that deal with smoothing data.
Method: Hodrick Prescott Filter
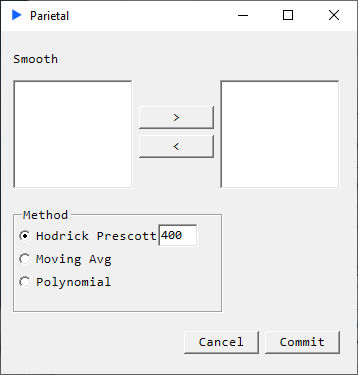
Description
Return a matrix that has been smoothed column-wise using the Hodrick Prescott filter. In other words, the HP filter extracts the trend component from a time series. Our implementation of the filter here makes two passes, forward and backward.
$$ \large min_{\tau}(\sum_{t=1}^T\left(y_t - \tau_t\right)^2 + \lambda \sum_{t=2}^{T-1}\left((\tau_{t+1} - \tau_t) - (\tau_t - \tau_{t-1})\right)^2) $$
Smoothing increases with increasing parameter value.
While quite prevalent in econometric work, James Hamilton warns against using HP filters[1]. Other econometricians seem to think there are times when its ok[2].
Returns
- Smoothed matrix. I.e. a matrix with trend components, cyclical components are ignored.
Method: Moving Average
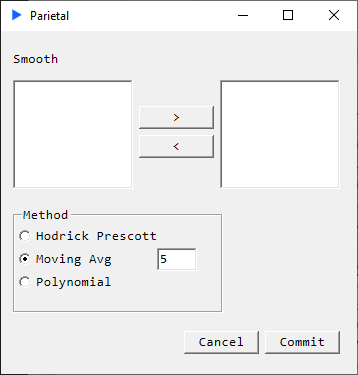
Description
Return a matrix that has been smoothed column-wise using a simple moving average.
Smoothing increases with increasing parameter value.
Returns
- Smoothed matrix.
Method: Polynomial
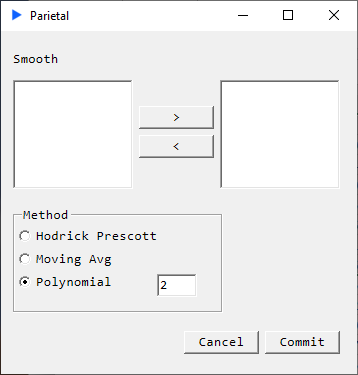
Description
Return a matrix that has been smoothed column-wise. The method fits a polynomial of a user specified order, decomposes the vector into trend and cycle components but only returns the trend component.
Smoothing increases with increasing parameter value.
A parameter value of 0 will simply return the means of the vectors.
Returns
- Smoothed matrix.