Dispersion Tests
Chi-Square Test for Variance
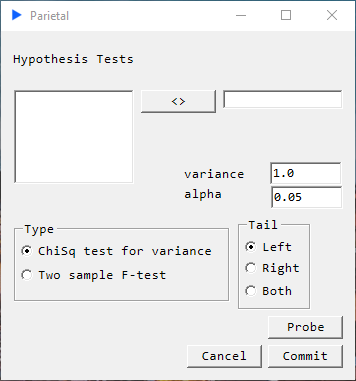
Description
Determines if the variance of a population is equal to a specified value.
| Tail | Alt. Hypothesis |
|---|---|
| $left\hspace{1cm}$ | $ H_{1}: \sigma^{2} \lt \sigma_{0}^{2} $ |
| $right\hspace{1cm}$ | $ H_{1}: \sigma^{2} \gt \sigma_{0}^{2} $ |
| $both\hspace{1cm}$ | $ H_{1}: \sigma^{2} \neq \sigma_{0}^{2} $ |
Returns
- p-value
- decision
- Chi-Sq statistic
F-Test for Two Variances
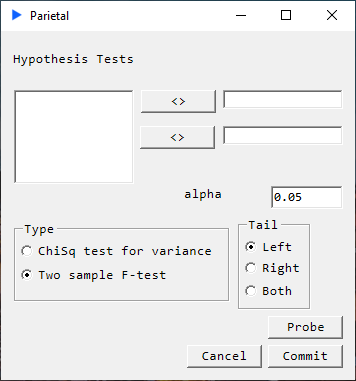
Description
Determines if the variances of two populations are equal.
| Tail | Alt. Hypothesis |
|---|---|
| $left\hspace{1cm}$ | $ H_{1}: \sigma_{1}^{2} \lt \sigma_{2}^{2} $ |
| $right\hspace{1cm}$ | $ H_{1}: \sigma_{1}^{2} \gt \sigma_{2}^{2} $ |
| $both\hspace{1cm}$ | $ H_{1}: \sigma_{1}^{2} \neq \sigma_{2}^{2} $ |
Returns
- p-value
- decision
- F statistic
Levene Test for Equal Variances
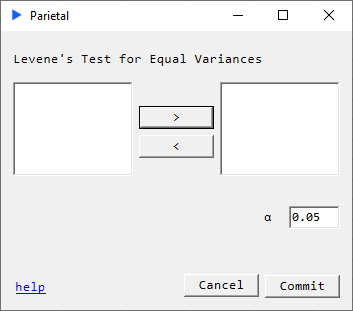
Description
Null hypothesis is that the population variances are equal.
The Levene test statistic is defined as: $$ W = \frac{(N-k)} {(k-1)} \frac{\sum_{i=1}^{k}N_{i}(\bar{Z}_{i.}-\bar{Z}_{..})^{2} } {\sum_{i=1}^{k}\sum_{j=1}^{N_i}(Z_{ij}-\bar{Z}_{i.})^{2} } $$
where $ Z_{ij} = |Y_{ij} - \bar{Y}_{i.}| $ and $ \bar{Y}_{i.} $ is the mean of the ith subgroup.
Often used to check the homogeneity of variances assumption before running an ANOVA.
Returns
- p-value
- decision
- F statistic
- degrees of freedom